STA SCHERZANDO MISTER FEYNMAN

 

"sta scherzando mister Feynman?" eh si!... É un po' come il latte o limone nel te'... "tutti e due!" giusto giusto la sera me ne rileggo un paio di capitoli Eh si !!!! Feynman è sempre spiritoso, ironico e ovviamente geniale : in questo particolare esperimento utilizza un soldato, un fucile mitragliatore e i suoi proiettili, riprendendo pari pari lo schema delle 2 fenditure. Il fucile è posto dietro a un foro fatto in una parete. L’arma, però, spara a casaccio in tutte le direzioni e non solo davanti a sé, lungo una linea fissa e determinata. Probabilmente è un’arma vecchia e sgangherata oppure il soldato è un po’ ubriaco. Meglio così, fa proprio al caso nostro. A una certa distanza davanti alla prima parete ne inseriamo un’altra, sempre di metallo e capace di fermare i proiettili che vi piombano addosso. In questa pratichiamo i due fori o -meglio- fenditure 1 e 2. Esse permetteranno di proseguire solo ai proiettili che le attraversano. Infine, a distanza ancora maggiore, poniamo un’altra parete di metallo, coperta con qualche materiale simile alla sabbia che intrappoli il proiettile che vi giunge. Questa permette di raccogliere i proiettili che l’hanno colpita e contarli, dopo aver sparato una raffica. Ovviamente, i proiettili escono dal fucile uno alla volta e quindi non possono urtarsi tra di loro, durante il viaggio, e nemmeno rompersi o dividersi in più pezzi. Conseguentemente, i proiettili che arrivano sulla sabbia lo fanno uno alla volta e sono perfettamente integri. Sembra una cosa ovvia, ma tenetela bene a mente. La Fig. 10 rappresenta la configurazione del nostro esperimento. Questa figura e la 13 e la 15 che seguiranno sono piuttosto approssimative, anche se più che sufficienti per definire il problema. Le uso perché credo (non ne sono completamente sicuro) siano proprio gli schizzi di Feynman. Alla meraviglia si aggiunge anche un po’ di emozione.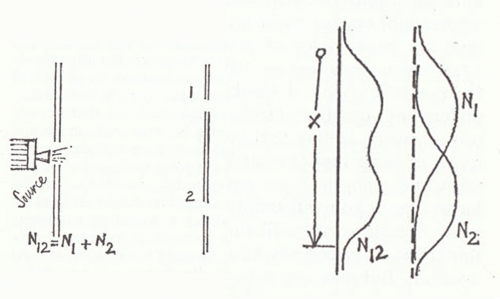

Diamo il via al soldato. Immaginiamo che la raffica sia stata lunghissima e che quindi abbia sparato un numero molto alto di proiettili (i grandi numeri sono fondamentali per parlare di probabilità). Contiamo i proiettili finiti nella sabbia in funzione della posizione che hanno. Anzi, facciamo qualcosa di ancora più raffinato matematicamente. Calcoliamo la percentuale di proiettili arrivati nelle diverse posizioni. In tal modo si ha immediatamente la probabilità che una certa posizione della lastra ha di essere raggiunta da un proiettile. Potevamo fare lo stesso in modo ancora più preciso. Mettere una “scatola” o un “barattolo” pieno di sabbia in posizioni sempre diverse della parete finale e sparare ogni volta 100 o 1000 o 10000 proiettili. Contare quanti ne giungevano nella scatola e stabilire la probabilità per la scatola in quella posizione. Poi facevamo scorrere la scatola in un altro punto (in modo continuativo e completo) e via con altri 100 o 1000 o 10000 colpi. Alla fine avevamo nuovamente la probabilità di ogni punto della parete di essere colpito a parità di colpi sparati. Insomma, la scatola può essere considerata un rivelatore di proiettili e quindi di probabilità.

In un modo o nell’altro possiamo facilmente disegnare la curva della probabilità in funzione di una certa coordinata x, che indica la posizione lungo la piastra di raccolta. Comunque, proiettili o probabilità che siano, la parete finale assomiglierebbe alla figura, dove le strisce scure sono le due zone maggiormente colpite. Al massimo due e non più di due.

Qualcuno potrebbe dire: “Perché non contare i proiettili, senza fare troppi passaggi matematici?” La risposta sarà ovvia alla fine dell’articolo. Abbiamo bisogno di parlare in termini di probabilità, dato che i proiettili che useremo dopo hanno un comportamento assai più strano di quello delle pallottole. La curva di probabilità ha una forma simile a quella segnata come N12. Ovviamente, se il soldato mirasse con precisione, i proiettili si troverebbero quasi esattamente dietro alle due fenditure. Invece è ubriaco, spara a casaccio e i proiettili entrano inclinati o toccano le pareti delle fenditure e rimbalzano. In altre parole, possono cadere nella scatola anche quando è spostata rispetto alle fenditure, pur se in numero minore. Ne segue che la linea della probabilità descrive una curva che ha due picchi in corrispondenza delle due fenditure (più o meno) e poi si smorza. Questa curva dipende molto dalla distanza tra le due fenditure, come vedremo tra poco.Cosa rappresenta la curva della probabilità N12? Sicuramente è la somma dei proiettili entrati attraverso 1 e quelli entrati attraverso 2, espressa come probabilità. E’ una cosa ovvia, pensando che ogni proiettile è un singolo oggetto perfettamente definito. In altre parole, il proiettile è visibile e localizzabile lungo tutto il suo percorso. Tenete bene a mente questa frase, mi raccomando. Per averne la certezza, però, basta fare una prova semplicissima (è meglio essere sicuri di ciò che facciamo perché tra poco l’apparenza ingannerà e come!). Chiudiamo la fenditura 2 e rifacciamo tutto l’esperimento. Otterremmo la curva di probabilità N1. Poi chiudiamo la fenditura 1 e ricominciamo tutto da capo. Si avrà la curva N2. Se il numero di colpi è sufficientemente alto, la statistica ci assicura che N12 è esattamente la somma di N1 più N2. Come già detto, ogni proiettile è un singolo oggetto e quindi il loro numero totale si ottiene sommando i proiettili che arrivano sulla scatola, indipendentemente dal fatto che provengano da 1 o da 2. Questo fatto si ripercuote pari pari sulla probabilità.Meglio essere ancora più semplici. Se spariamo cento colpi con solo la fenditura 1 aperta e poniamo la scatola con la sabbia in una certa posizione, verifichiamo, ad esempio, che soltanto 10 proiettili l’hanno centrata. La probabilità è quindi data da 10/100. Chiudiamo 1 e apriamo 2, mantenendo, però, la scatola di sabbia sempre nella stessa posizione. Questa volta attraverso 2 arriveranno sulla scatola solo 4 proiettili su 100 sparati. Il che vuol dire una probabilità del 4/100. Possiamo quindi dire che la probabilità di avere un proiettile nella scatola è il 10% attraverso la fenditura 1 e il 4% attraverso la fenditura due. Apriamole ora entrambe e spariamo nuovamente 100 colpi con la scatola (svuotata) sempre nella stessa posizione. E’ ovvio che 10 proiettili arriveranno sulla scatola attraverso 1 e soltanto 4 attraverso 2. In totale avremo 14 proiettili, su 100 sparati, finiti nella scatola. La probabilità è allora del 14%, proprio uguale alla somma delle probabilità ottenute aprendo singolarmente le due fenditure. Ricapitolando, la probabilità relativa ai proiettili che provengono da entrambe le fenditure è uguale alla somma delle probabilità relative a ogni singola fenditura. Ne deriva, quindi, che il valore massimo della somma delle probabilità delle singole fenditure (ossia la massima probabilità con entrambe le fenditure aperte) può verificarsi anche nel punto medio tra di loro, se queste sono molto vicine. Lo vediamo nella Fig. 12, per varie posizioni. Comunque, questo è un problema decisamente secondario che ho toccato solo per non creare una confusione del tutto inutile e spiegabilissima: ce ne saranno di ben più importanti. I massimi di probabilità possono essere due o diventare uno solo, ma questo dipende solo dalla distanza tra le fenditure e non dal comportamento dei proiettili. Attenzione, quindi a non confondere questo risultato con la frangia d’interferenza luminosa che è sempre al centro delle due fenditure. La cosa veramente importante nel caso dei proiettili è che la curva somma rimane sempre uguale alla somma delle curve singole.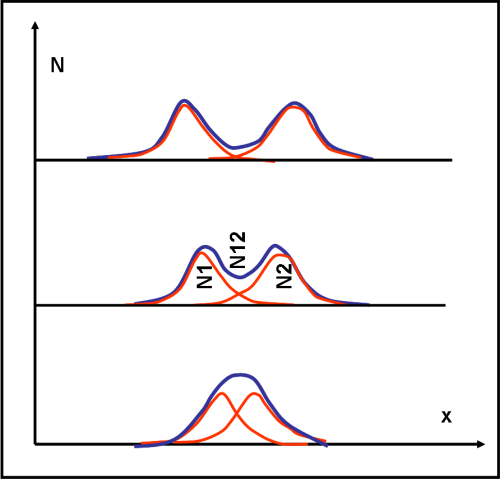

Questo risultato appare ovvio e addirittura “stupido” a tutti noi abituati a vivere la realtà quotidiana. Tuttavia, descrive un fenomeno che diventerà ben più importante tra poco: non vi è stata interferenza, ossia i proiettili non si sono disturbati reciprocamente (d’altra parte non potevano farlo, secondo la nostra logica). Nell’esperimento appena fatto, i proiettili escono, infatti, uno alla volta e non si possono urtare tra loro. Chi arriva arriva, e il suo destino è indipendente da quello che fanno gli altri. Quanto è importante la parola “indipendente”! E quanto è legata alla nostra visione logica del mondo.

Fatemi scrivere una banale formula, che ci sarà utile per confrontarla con quelle (pochissime) successive.

N12 = N1 + N2 nessuna interferenza

Passiamo adesso alle onde marine o qualcosa del genere. Abbiamo già parlato di questa situazione, ma non è male ripeterla sia per non interrompere la sequenza logica ideata da Feynman, sia perché tornare su certi concetti non fa mai male.

Una piscina bucata

La sorgente adesso non è più il fucile, ma una grande massa d’acqua, che preme dietro la prima parete. In quella parete c’è un foro, da cui l’acqua riesce a passare e si riversa al di là del muro. Lo fa producendo un’onda composta di creste e depressioni (massimi e minimi). Per causare un’onda, basta che si agiti l’acqua prima della parete: più viene agitata e più l’onda aumenta. Per essere più esatti, si origina un treno di onde, una dietro l’altra, separate tra loro da quella che viene chiamata lunghezza d’onda (distanza tra due creste o tra due depressioni). Ad un certa distanza poniamo nuovamente la parete con le due strette fenditure, come nel caso dei proiettili. L’onda che si è formata dopo la prima apertura colpisce la seconda parete e riesce ad attraversarla dove ci sono le due fenditure. Cosa succede a questo punto? L’onda, passando dalle fenditure, si divide in due nuove onde che mantengono la stessa lunghezza di quella originaria. In altre parole, è come dire che, se l’apertura è abbastanza piccola, essa dà origine a una nuova onda che si propaga da lei, come se si fosse scagliato un sasso proprio in quel punto. Di questo comportamento avevamo già parlato a proposito della luce. In realtà, al posto dell’acqua potremmo considerare onde luminose (come ha fatto Young) e otterremmo lo stesso risultato, almeno apparentemente e a una prima visione sommaria.

Torniamo alle due onde originatesi nelle due fenditure. Esse proseguono verso la terza parete dove prima avevamo messo la sabbia per i proiettili. Adesso, dobbiamo cambiare rivelatore. Scegliamo, ad esempio un tappo di sughero. Quando l’onda arriva sull’ultima parete lui si alza e si abbassa seguendo le creste e le depressioni. L’esperimento si vede in Fig. 13. Come abbiamo fatto prima, con la scatola piena di sabbia, spostiamo il tappo lungo tutta la parete e vediamo come varia l’altezza che riesce a raggiungere. In realtà, ciò che a noi interessa è l’energia che viene rilasciata dall’onda al tappo o -sepreferite- la sua intensità.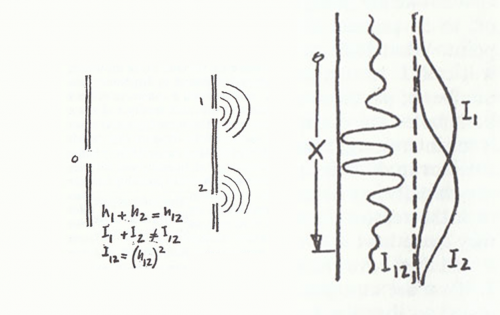

Stiamo attenti a non confondere l’ampiezza di un onda con la sua intensità. Nel caso del fucile, energia rilasciata e proiettile erano praticamente la stessa cosa, dato che ogni proiettile rilasciava la stessa energia. Per le onde, la situazione è leggermente più complicata. Si può dimostrare (non lo facciamo perché bisognerebbe eseguire parecchi calcoli matematici, però credeteci!) che l’intensità è proporzionale al quadrato dell’altezza. D’altra parte a noi interessa proprio l’intensità o energia rilasciata, per confrontarla, ad esempio, con quella della luce o dei proiettili. La curva finale, in funzione della posizione del tappo lungo la parete, è ben più strana della N12 del caso precedente. Ciò che si vede è una figura che sembra anch’essa un’onda, un continuo sali e scendi, senza nessuna relazione con la posizione delle due fenditure. O -meglio- dipendente dalla distanza tra loro, nel senso che l’oscillazione che si nota sulla parete può stringersi o allargarsi. La struttura a strisce, però, non cambia. Il risultato (lo conosciamo bene) non è altro che il fenomeno dell’interferenza delle onde. E’ estremamente simile a quello ottenuto da Young con la luce. D’altra parte Young aveva detto che la luce si propagava per onde proprio perché il suo comportamento era uguale a quello delle onde marine. Anche questa seconda fase dell’esperimento è di una banalità quasi sconcertante e nuovamente ovvia. Ma… Feyman è davvero un genio? Aspettate, aspettate… Ricordiamo ancora che nel caso dei proiettili vi erano poche scelte: o arrivava o non arrivava. Nel caso dell’onda, l’energia o intensità dell’onda può assumere tutti i valori compresi tra un massimo e lo zero (acqua piatta). Chiamiamo la curva finale, che descrive la figura d’interferenza, I12. Questa volta, però, per ottenere la curva I12, non possiamo sommare le energie rilasciate al tappo con l’acqua che passa da una sola fenditura aperta, come succedeva nel caso dei proiettili. Per provarlo basta tappare prima 2 e poi 1. Si ottengono separatamente le curve I1 e I2, curve che assomigliano a quelle dei proiettili sparati dal fucile attraverso una sola apertura. Questo è ovvio (rimanendo nella fisica classica) dato che se l’onda passa da una sola fenditura non può interferire con un’altra e quindi ha un comportamento apparentemente simile a quello dei proiettili: un picco che si smorza, allontanandosi dalla direzione centrale, in quanto l’onda perde di intensità. La massima intensità la mostra proprio dove “sbatte” per la prima volta contro la parete. Nel caso dell’interferenza, abbiamo, invece, diversi massimi e minimi (basta considerare una qualsiasi linea parallela alla parete e si vede chiaramente che i massimi e i minimi sono molteplici). 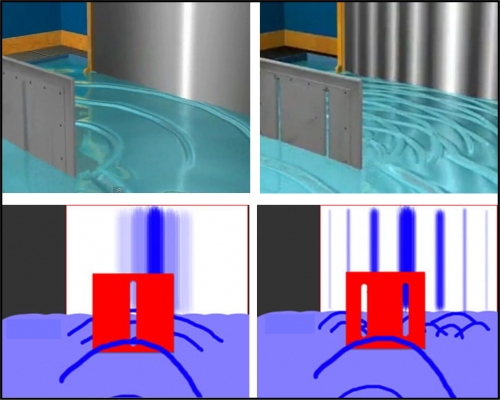L’unica differenza sostanziale tra proiettili passanti da una singola fenditura e onda proveniente anch’essa da una sola apertura è che i proiettili, o -meglio- l’energia rilasciata o, se volete, l’intensità del numero di proiettili, è praticamente il loro numero, nel caso dell’onda l’intensità è proporzionale al quadrato dell’altezza, ossia I1 = h12 e I2 = h22. Dobbiamo paragonare altezze e numero di proiettili, dato che sono le grandezze che rileviamo e che indicano la probabilità finale.

Sappiamo però che le altezze delle onde si sommano e vale la relazione: h1 + h2 = h12. Per l’intensità, ossia per l’energia data al tappo, con entrambe le fenditure aperte, si ha quindi (l’intensità va con il quadrato dell’altezza):

I12 = h122 = (h1 + h2)2 e, sicuramente:

I12 ≠ I1 + I2 interferenza

Bisogna riflettere bene su questa conclusione che, in pratica, fornisce la migliore descrizione della differenza tra onde e di particelle. Queste ultime non mostrano alcun fenomeno di interferenza e la probabilità di trovare una particella in un certo punto con entrambe le fenditure aperte è esattamente la somma delle probabilità di trovare una particella in quello stesso punto chiudendo una fenditura alla volta (N12 = N1 + N2). Le onde mostrano invece un risultato finale diverso. L’intensità dell’onda risultante, a fenditure aperte, non è la somma delle intensità a fenditure alternativamente chiuse. Non è difficile considerare l’intensità come la probabilità di alzarsi di più o di meno del tappo. Rifletteteci un attimo e la cosa diventerà ovvia.

Questo esperimento, che abbiamo fatto con l’acqua, è praticamente lo stesso che Young aveva fatto con la luce. Egli aveva trovato le frange di interferenza e aveva potuto concludere che la luce non poteva essere trasmessa attraverso particelle (proiettili) dato che causava interferenza. Feynam, per adesso, ha solo dato una definizione “matematica” e concettuale della differenza tra onde e particelle che colpiscono un muro.